우리 학과 핵융합 및 플라즈마 연구실의 김영철 교수팀은 정세민 박사과정이 1저자로 참여하여 핵융합에 필요한 1억도 플라즈마를 제어하기 위한 자기장 구조를 실시간으로 재구성하는 인공신경망 기반 알고리즘을 개발하였다. 이는 핵융합 관련 top 저널 중 하나인 Nuclear Fusion 에 게재 승인되었다. (DOI:https://doi.org/10.1088/1741-4326/ab555f)

핵융합 플라즈마를 가두고 제어하는 장치인 토카막은 플라즈마 상태를 자기장 구조와 함께 재구성함으로써 실시간 운전을 할 수 있으며 이 자기장 구조 재구성을 토카막 평형상태 재구성이라 일컫는다. 토카막 평형상태 재구성은 보통 플라즈마의 유체적 현상을 기술하는 Magnetohydrodynamics (MHD) 수식으로 부터 정상상태 가정 등을 통해 얻은 Force-balance 식을 이용한다. 이 Force-balance 식과 전자기장을 기술하는 맥스웰방정식에서 유도된 Grad-Shafranov 식을 통해 토카막 평형 상태를 재구성한다. 따라서 일반적으로 Grad-Shafranov 식의 해를 구했다 라는 것은 토카막의 평형 상태를 재구성했다는 말을 의미한다.

그러나 이 Grad-Shafranov 식은 2계 비선형 미분방정식으로 해를 구하기 위해서 일반적으로 수치적 해석 방법론이 요구된다. 이는 해당 식의 해를 실시간 운전 중에 구하기 어렵게 만드는 요소 중 하나이며, 이를 해결하기 위해 수치적 반복 계산을 한차례만 수행하는 등의 요소들이 도입되곤 하였다.

본 논문에서는 반복계산 횟수의 제한 등을 통한 수동적인 방법론으로 해결하는 것이 아닌 능동적인 방법으로써 인공신경망을 사용, Grad-Shafranov 식의 해를 구할 수 있는 신경망을 구현하였다. 여기서 신경망은 일종의 강력한 Grad-Shafranov 식의 가설 모델로 취급되며, 신경망의 출력 값에 대한 2계 비선형 해석적 미분은 Grad-Shafranov 식을 따를 것이다 라는 혁신적인 아이디어에 근거한다.

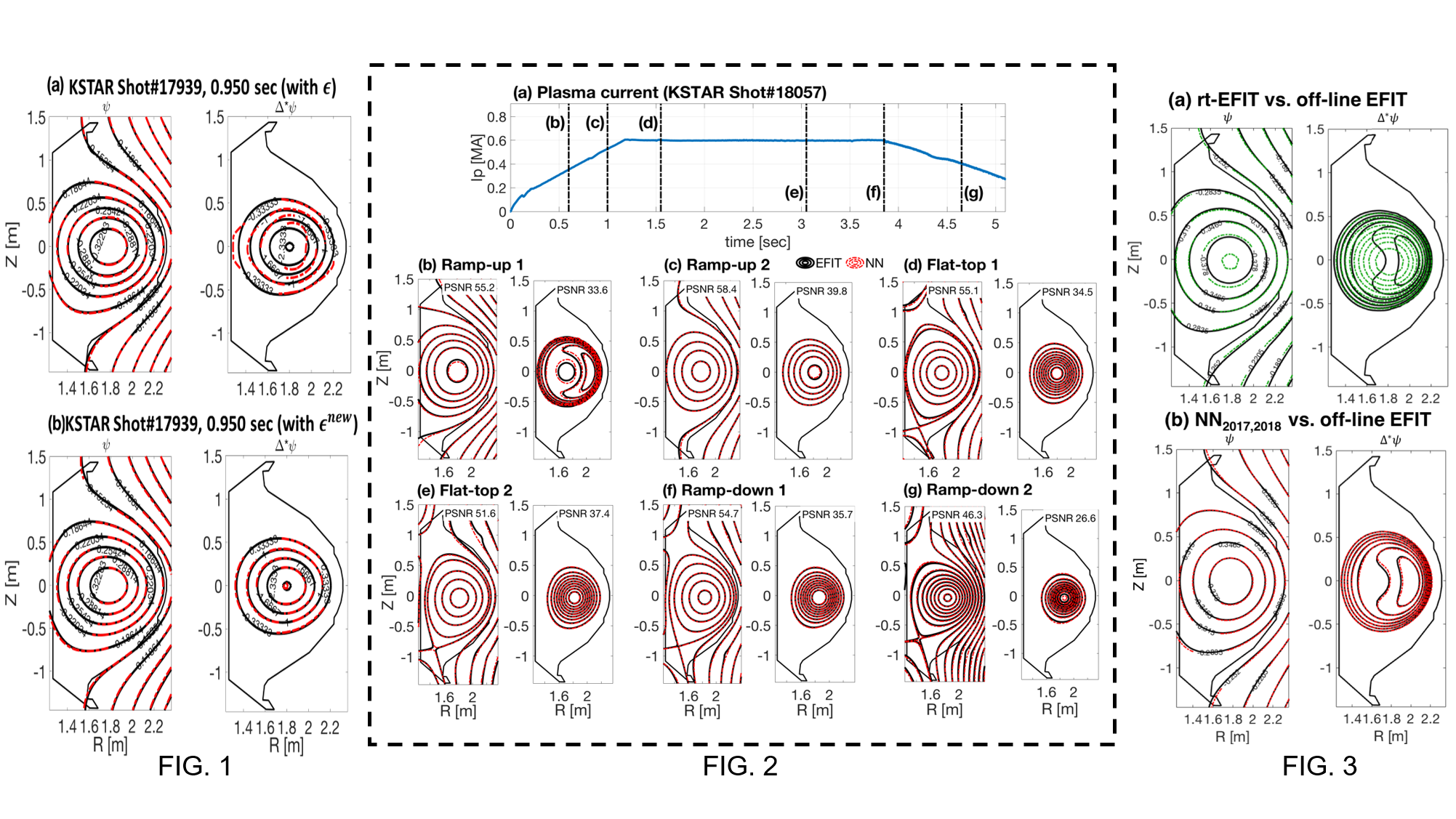
즉, 기존 신경망 훈련 방법인 ‘신경망의 출력 값만에 대한 훈련’ 은 그 값의 미분에 대한 부정확성을 야기하며 (그림 1 (a)), 이 사실은 훈련된 신경망이 ‘Grad-Shafranov 식을 따를 것이다’ 라는 가설에 위배된다는 결과를 보여준다. 따라서 우리는 그림 1 (b) 처럼, ‘신경망 출력 값 뿐만이 아닌 해당 값의 미분 값 또한 훈련’ 함으로써 우리의 가설을 만족하는 결과를 얻어냈으며, 신경망이 실제 토카막 운전 상황에 사용될 수 있음을 그림 2 를 통해 나타내었다. 또한, 우리의 신경망은 기존의 수동적 방법론으로 구해낸 평형과 (그림 3 (a)) 달리, 보다 더 정확한 평형상태를 (그림 3 (b)) 실시간으로 재구성할 수 있는 우수성을 입증하였다.

본 논문을 토대로 개발된 기술이 보다 정밀한 토카막 운전에 도움이 될 것으로 기대하는 바이다